Bipin's Bubble
Kalman Variational Auto-Encoders
arxiv link to paper: https://arxiv.org/abs/1710.05741
This paper is another paper that deals with modelling dynamic systems. Realated earlier post on Deep Variational Bayes Filters along with state space posts on Deep Kalman Filters and VRNN.
This is a paper summary and notes written by me during reading this paper. I claim no rights to any intellectual property in this post. I am sharing this mostly for personal purposes and just in case someone might find my personal notes helpful
Introduction
- The basic idea of this paper is that the observation in time series are generated from a latent variable, and the latent variable changes dynamically.
- Model observation to latent encoding by VAE, and model dynamics of latent variable as Linear Gaussian SSM.
Modelling assumptions
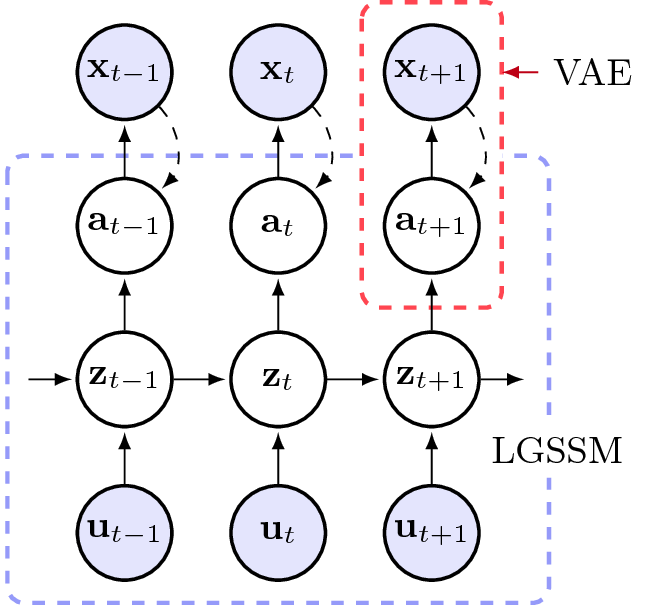The image is taken from github implementation of the code for this project by
its authors: Simon Kamronn and is available publically in their github:
simonkamronn/kvae
- In th graphical model in the image:
- $x_t$ is observation at time t.
- $a_t$ is latent state of $x_t$ at time t.
- $z_t$ is dynamically changing latent state for $a$
- $\gamma$ are parameters of LG-SSM
- $\theta$ are parameters of generative model.
Generative Modelling for x
From the Graphical Model we can easily factorize the generative model for x as:
\[p_\theta(\vec{x}|\vec{a}) = \prod_{t=1}^{T} p_\theta(x_t | a_t)\]The vector $\vec{a}$ is also assumed to follow a prior distribution given as: \(\begin{align} p_\gamma(\vec{a}|\vec{u}) &= \int p_\gamma(\vec{a}, \vec{z} | \vec{u}) \ d\vec{z} &= \int p_\gamma(\vec{a} | \vec{z}, \ \vec{u}) \ p_\gamma(\vec{z}| \vec{u}) \ d\vec{z} \end{align}\)
Dynamics model: LGSSM
For Linear Gaussian State Space Modelling (LG-SSM) assumption for dynamics of $a$ with latent state $z$, we can write the modelling assumptions as:
\[p_{\gamma_t}(\vec{z_t} | \vec{z}_{t-1}, \vec{u_t}) = \mathcal{N} (\vec{z_t}; \ \mathbf{A}_t\vec{z}_{t-1} \ + \ \mathbf{B}_t\vec{u}_{t}, \ \ \ \mathbf{Q}) \\ , \\ p_{\gamma_t}(\vec{a_t} | \vec{z}_{t}) = \mathcal{N} (\vec{a_t}; \ \mathbf{C}_t\vec{z}_{t}, \ \ \ \mathbf{R}) \\\]Where, $\gamma_t = [\mathbf{A}_t, \mathbf{B}_t, \mathbf{C}_t]$
Learning
The marginal of $x$ under this graphical model can be obtained by marginalizing the joint with both $a$ and $z$ as:
\[\begin{align} p(\vec{x} | \vec{u}) &= \int \int p(\vec{x}, \vec{a}, \vec{z} | \vec{u}) d\vec{a} \ d\vec{z} \\ &= \int \int p(\vec{x}| \vec{a}, \vec{z}, \vec{u}) \ p(\vec{a} | \vec{z} \ \vec{u}) p_\gamma(\vec{z} | \vec{u}) d\vec{a}\ d\vec{z} \\ &= \int \int p_\theta(\vec{x}| \vec{a}) \ p_\gamma(\vec{a} | \vec{z}) p_\gamma(\vec{z} | \vec{u}) d\vec{a}\ d\vec{z} \\ &= \int \int p_\theta(\vec{x}| \vec{a}) \ p_\gamma(\vec{a} | \vec{z}) p_\gamma(\vec{z} | \vec{u}) d\vec{a}\ d\vec{z} * \dfrac{q_\phi(\vec{a},\ \vec{z} \ | \vec{x},\ \vec{u})}{q_\phi(\vec{a},\ \vec{z} \ | \vec{x},\ \vec{u})}\\ \end{align}\]Taking log on both sides result in:
\[\begin{align} log \ p(\vec{x} | \vec{u}) &= log \ \int \int p_\theta(\vec{x}| \vec{a}) \ p_\gamma(\vec{a} | \vec{z}) p_\gamma(\vec{z} | \vec{u}) d\vec{a}\ d\vec{z} * \dfrac{q_\phi(\vec{a},\ \vec{z} \ | \vec{x},\ \vec{u})}{q_\phi(\vec{a},\ \vec{z} \ | \vec{x},\ \vec{u})}\\ &\ge E_{q_\phi(\vec{a},\ \vec{z} \ | \vec{x},\ \vec{u})}[ log \ \dfrac{p_\theta(\vec{x}| \vec{a}) \ p_\gamma(\vec{a} | \vec{z}) \ p_\gamma(\vec{z} | \vec{u})}{q_\phi(\vec{a},\ \vec{z} \ | \vec{x},\ \vec{u})}] \end{align}\]The ELBO is clearly a function of all three: $\theta, \gamma, and, \phi$
The approximate joint can be further factorized based on the Graphical Model as:
\[q_\phi(\vec{a},\ \vec{z} \ | \vec{x},\ \vec{u}) = q_\phi(\vec{a},\ | \vec{x}) * q_\phi(\vec{z} \ | \vec{a},\ \vec{u}) \\ = \prod_{t=1}^T q_\phi(a_t | x_t) * q_\phi(\vec{z} \ | \vec{a},\ \vec{u})\]Using this ELBO can be simplified as:
\[\begin{align} ELBO = \mathcal{f} (\theta, \gamma, \phi) &= E_{q_\phi(\vec{a},\ \vec{z} \ | \vec{x},\ \vec{u})}[ log \ \dfrac{p_\theta(\vec{x}| \vec{a}) \ p_\gamma(\vec{a} | \vec{z}) \ p_\gamma(\vec{z} | \vec{u})}{q_\phi(\vec{a},\ \vec{z} \ | \vec{x},\ \vec{u})}] \\ &= E_{q_\phi(\vec{a},\ \vec{z} \ | \vec{x},\ \vec{u})}[ log \ \dfrac{p_\theta(\vec{x}| \vec{a}) \ p_\gamma(\vec{a} | \vec{z}) \ p_\gamma(\vec{z} | \vec{u})}{q_\phi(\vec{a},\ | \vec{x}) * q_\phi(\vec{z} \ | \vec{a},\ \vec{u})}] \\ &= E_{q_\phi(\vec{a}, \ | \vec{x})}[ E_{q_\phi(\vec{z} \ | \vec{u})}[ log \dfrac{ p_\theta(\vec{x}| \vec{a}) \ }{ q_\phi(\vec{a},\ | \vec{x}) } + log \dfrac{ p_\gamma(\vec{a} | \vec{z})\ p_\gamma(\vec{z} | \vec{u}) }{ q_\phi(\vec{z} \ | \vec{a},\ \vec{u}) } ] ]\\ &= E_{q_\phi(\vec{a}, \ | \vec{x})}[ E_{q_\phi(\vec{z} \ | \vec{u})}[ log \dfrac{ p_\theta(\vec{x}| \vec{a}) \ }{ q_\phi(\vec{a},\ | \vec{x}) } ] + E_{q_\phi(\vec{z} \ | \vec{u})}[ log \dfrac{ p_\gamma(\vec{a} | \vec{z})\ p_\gamma(\vec{z} | \vec{u}) }{ q_\phi(\vec{z} \ | \vec{a},\ \vec{u}) } ] ]\\ &= E_{q_\phi(\vec{a}, \ | \vec{x})}[ log \dfrac{ p_\theta(\vec{x}| \vec{a}) \ }{ q_\phi(\vec{a},\ | \vec{x}) } + E_{q_\phi(\vec{z} \ | \vec{u})}[ log \dfrac{ p_\gamma(\vec{a} | \vec{z})\ p_\gamma(\vec{z} | \vec{u}) }{ q_\phi(\vec{z} \ | \vec{a},\ \vec{u}) } ] ] \end{align}\]Optimizing this ELBO makes it possible to learn the dynamic system.
References
- [1] M. Fraccaro, S. Kamronn, U. Paquet, and O. Winther, “A Disentangled Recognition and Nonlinear Dynamics Model for Unsupervised Learning,” in Advances in Neural Information Processing Systems, 2017, vol. 30. Accessed: Apr. 27, 2022. [Online]. Available: https://proceedings.neurips.cc/paper/2017/hash/7b7a53e239400a13bd6be6c91c4f6c4e-Abstract.html