Probability 3: Structured Probabilistic Models

The chapter 2 of Deep Learning Book is focussed on Probability and Information Theory. This post is TLDR part 3 of the corresponding chapter of the book.

Background

• ML algorithms involve large number of random variables.
  • Joint Probability distribution of these many variables is complex.
  • Often, very few variables interact with each other directly.
  • Using joint probabilities to describe everything is inefficient.
• Alternative: Factorizing joint probabilities into conditionals of interacting variables.
  • Advantage: Less number of parameters
  • Efficient representation
  • Can be represented as graphs called: graphical models

\[p(a,b,c) = p(z) p(b \ \vert a) p(c \ \vert b)\]

• Recall: Graphs: set of vertices connected to each other with edges.
  • A graph $G$ with set of vertices $V$ and edges $V_{i,j}$
  • Can be directed or undirected.
• Probabilities can be represented as graphs: directed or undirected.
  • Each node corresponds to a random variable.
  • Edges between nodes represent the direct interaction between the random variables represented by those nodes.

---

Directed Graph models

• Graphs with directed edges
• They represent factorizations into conditional probabilities
• Contains one factor for every random variable $x_i$ in the distribution (one vertrex for each random variable)

• That factor consists of conditional distribution for over $x_i$ given parents of $x_i$ denoted as: $P_{a_G}(x_i)$

  \[p(\mathbf{x}) = \underset{i}{\operatorname{\prod}} \ {p(x _i \ \vert \ P_{a_G}(x_i))}\]
• Example:

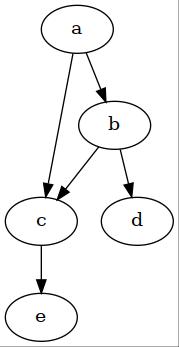
In the above directed graph, the joint probability of random variables: $a,b,c,d,e$ can be written as:

\[p(a,b,c,d,e) = p(a) p(b \vert a) p(c \vert a, b) p(d \vert b) p(e \vert c)\]

---

Undirected Graph models

• Factorize joint into functions, instead of conditionals.
• Set of nodes connected to each other in graph $G$ is called clique
• Each clique $C^{(i)}$ is associated with a factor $\phi^{(i)}(C^{(i)})$
• These factors are functions and not probabilities.
• Output of these functions must be non-negative.
  • If they were probabilities as in directed, they would also integrate to 1.
• Probability of any configuration is proportional to product of all these factors.
  • The proportanility is converted to equality by a normalizing constant that ensures that the total probability sums to one.

\[p(\mathbf{x}) = \frac{1}{Z} \underset{i}{\prod} \phi^{(i)}(C^{(i)})\]

• Example:

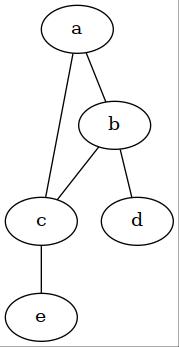
In the above undirected graph, the joint probability of random variables: $a,b,c,d,e$ can be written as:

\[p(a,b,c,d,e) = \frac{1}{Z} \phi^{(1)}(a,b,c) \phi^{(2)}(b,d) \phi^{(3)}(c, e)\]

---

Notes

• Graphical models are just different ways of representing the probability representations.
• The choise of method is not mutually exhaustive: different representations can be used for representing the same thing in different ways.
• Same probability distribution can be represented as directed as well as undirected depending on the situation.

---

September 25th, 2020 by Bipin Lekhak